در مدلاسیون دیجیتال ، یک سیگنال حامل آنالوگ به وسیله سیگنال های گسسته مدوله می شود . روش های مدلاسیون دیجیتال می تواند همانند مبدل های آنالوگ به دیجیتال باشد و بر طبق آن دِملاسیون مانند مبدل های دیجیتال به آنالوگ هستند. تغییرات در سیگنال خامل بر اساس اعداد محدود ( الفبای مدلاسیون) انتخاب می شود .
بر طبق تعریف سیگنال دیجیتال ، سیگنال مدوله شده به این روش نیز دیجیتال محسوب می شود .
تئوری نمونه برداری
این تئوری حداقل میزان نمونه برداری از یک سیگنال آنالوگ را تاجایی که اطلاعات اولیه آن سیگنال حفظ شود تعیین میکند. فرکانس نمونه برداری (fs) باید بیش از دو برابر بالاترین فرکانس سیگنال آنالوگ (fa) باشد. fs>2fa
تبدیل آنالوگ به دیجیتال
نمونه برداری
یک فرکانس KHZ8 به طور مثال برای نمونه برداری باند صوتی تلفن (3400-300 هرتز) انتخاب شده است، به عبارت دیگر سیگنال 8000 بار در ثانیه نمونه برداری میشود. فاصله زمانی بین دو نمونه متوالی از یک سیگنال از رابطه زیر محاسبه میشود.
µs 125 =8000/1Ta=1/fa
درشکل زیر چگونگی انتقال سیگنال از طریق یک فیلتر پایین گذر به یک سوئیچ الکترونیکی نشان داده شده است. فیلتر پایین گذر باند فرکانسی را محدود میسازد بطوریکه فرکانسهای بالاتر از نصف فرکانس نمونه برداری را حذف میکند. سوئیچ الکترونیکی بافرکانس HZ8000 از سیگنالها در هرs 125 نمونه بر میدارد. بنابراین خروجی حاصل از سوئیچ الکترونیکی یک سیگنال PAM میباشد.
8 khz
کوانتیزه کردن
سیگنالهای PAM هنوز به صورت آنالوگ میباشند. چون ارسال نمونهها بطریق دیجیتال سادهتر میباشد دراولین مرحله تبدیل سیگنالهای PAM به سیگنالهای دیجیتال PCM، آنها را کوانتیزه میکنیم بطوریکه تمام دامنه به فواصل کوانتیزه تقسیم میشود. اصول کوانتیزه کردن در شکل زیر مشاهده میشود.
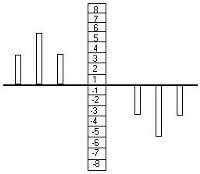
تعداد 16 فاصله کوانتیزه در شکل دیده میشود. این فاصلهها در محدوده مثبت 1+ تا 8+ ودر محدوده منفی از 1ـ تا 8ـ تقسیم شده است وبرای هر نمونه مقدار کوانتیزه مناسبی انتخاب شده است.
مرزهای تصمیم گیری حد فاصل بین مرزهای مجاور را مشخص میکند. بنابراین در جهت ارسال، مقادیر آنالوگ متعددی در یک فاصله کوانتیزه قرارمیگیرند. در جهت دریافت یک مقدار ثابت آنالوگ برای هر سیگنال که برابر با نقطه میانی فاصله کوانتیزه است، به دست میآید. این عمل باعث میشود تفاوتهایی بین نمونه سیگنالهای اولیه در جهت ارسال و مقادیر بازیابیشده در طرف دریافت به وجود بیاید. بطوریکه این اختلاف میتواند تا نصف یک فاصله کوانتیزه باشد. این اعوجاج به صورت نویز که منطبق بر سیگنال اصلی است ظاهر میشود. این اعوجاج کوانتیزاسیون با ازدیاد فواصل کوانتیزه کمتر میشود .
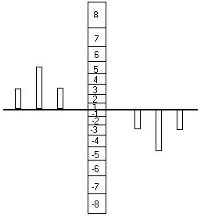
اگر فواصل کوانتیزه برای تمامیرنج دامنه یکسان باشد، درسیگنالهای با دامنه کوچکتر خطاهای بزرگتری به وجود میآید که این خطاها میتواند به اندازه سیگنالهای ورودی باشد و نسبت سیگنال به نویز کوانتیزاسیون آنقدر بزرگ نخواهد بود و به همین دلیل عملاً 256 فاصله کوانتیزه نامساوی به کار گرفته میشود.
(Non-Uniform Quantizing) در کوانتیزه غیریکنواخت فواصل کوانتیزه کوچکتر برای سیگنالهای کم دامنه وفواصل کوانتیزه بزرگتر برای سیگنالهای با دامنه بیشتر به کار رفته است. بنابراین نسبت سیگنال ورودی به خطای ممکن که از کوانتیزه نتیجه میشود تقریباً برای تمامیسیگنالهای ورودی یکسان خواهد بود.
CCITT دو نوع مشخصه برای کوانتیزاسیون غیریکنواخت توصیه کرده است.
- قانون Aبرای PCM30 که 13 قسمتی است و در آسیا واروپا به کار رفته است.
- قانون B برای PCM24 که 15 قسمتی است و در آمریکا و ژاپن به کار رفته است.
کد بندی
سیگنال PCM از کد کردن فواصل کوانتیزه شده به دست میآید. در شکل زیر محور عرضها، فواصل کوانتیزه مثبت را از 1 الی 128 و فواصل کوانتیزه منفی را از 1ـ الی 128ـ نشان داده است. دامنه سیگنال ورودی روی محور عمودی نشان داده شده است.
128
7
7-
به هر خط شکسته یک Segment میگوییم. هر Segment را به تعدادی Step تقسیم کردهایم.
| Segment | NO.Of Step |
| 1 | 0-32 |
| 2 | 33-48 |
| 3 | 49-64 |
| 4 | 65-80 |
| 5 | 81-96 |
| 6 | 97-112 |
| 7 | 113-128 |
کُدر الکترونیک یک کلمه PCM هشت بیتی را به ازای هر کدام از نمونهها نشان داده است. این کلمه PCM با فاصله کوانتیزه شده معین مرتبط است.
یک کد باینری 8 رقمی برای نشان دادن هر یک از 128 فاصله کوانتیزه مثبت ویا منفی، از مجموعاً 256 = 28 فاصله اختصاص یافته است پس هر کلمه PCM دارای 8 بیت میباشد. بیت اول تمامیکلمات PCM به کار رفته در فواصل کوانتیزه مثبت یک بوده و همین بیت برای کلمات PCM به کار رفته در فواصل کوانتیزه منفی صفر میباشد. بیتهای شماره 2و4و6و8 از هرکلمه PCM در هنگام انتقال معکوس میشود.
Wander & Jitter
اگر فرستنده و گیرنده دقیقاً باهم همزمان نباشند مشکلاتی از قبیل Wander و Jitter ایجادمیشود. اندازه Wander بالاتر از 10 هرتز میباشد و باعث میشود که موج در جای اصلی خودش در گیرنده دریافت نشود و گاهی موجب از دست رفتن چند مالتیفریم میشود که کلاک دقیقتر این مشکل را حل میکند.
انداره Jitter کمتر از 10 هرتز میباشد و باعث میشود موج در جای اصلی خودش دریافت نشود. این مشکل به راحتی با کلاک دقیق قابلحل میباشد.
روش های مدلاسیون دیجیتال بنیادی
بیشتر تکنیک های مدلاسیون دجیتال بنیادی بر پایه کلید زنی هستند :
هر کدام از این مدلاسیون ها زیر مجموعه ای دارند که بر حسب نیاز توسعه پیدا کرده اند
لیست تکنیک های مدلاسیون های دیجیتال معمول
کلید زنی شیفت فازی (PSK)
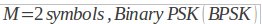
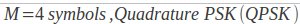
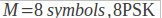
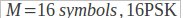
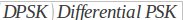

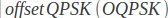

کلید زنی شیفت ـ فرکانس (FSK)
- Audio frequency-shift keying – AFSK
- Multi-frequency shift keying – M-ary FSK or MFSK
- Dual-tone multi-frequency – DTMF
- Dual-tone multi-frequency – DTMF
کلید زنی شیفت ـ دامنه (ASK)
- On-off keying (OOK), the most common ASK form
- M-ary vestigial sideband modulation, for example 8VSB
- Quadrature amplitude modulation (QAM) – a combination of
- PSK and ASK:Polar modulation like QAM a combination of PSK and ASK
روش مدلاسیون پالس مداوم (CPM)
Minimum-shift keying – MSK
Gaussian minimum-shift keying – GMSK
تسهیم تقسیم فرکانس متعامد (OFDM)
- discrete multitone (DMT) – including adaptive modulation andbit-loading.
- Wavelet modulation
- Trellis coded modulation (TCM), also known as trellis modulation
- Spread-spectrum techniques :
- Direct-sequence spread spectrum – DSSS
- Chirp spread spectrum (CSS) according to IEEE 802.15.4a CSS uses pseudo-stochastic coding
- Frequency-hopping spread spectrum (FHSS) applies a special scheme for channel release
در QAM، یک سیگنال هم فاز ( برای مثال یک سیگنال Cosine) و یک سیگنال با 1/4فاز ( مثلاً یک سیگنال sine) با مدلاسیون دامنه در دو حالت ( دو وضعیت) مقدار محدود دامنه مدوله و با هم جمع می شوند . در این صورت به نظر می رسد که یک سیستم دو گانه است که هر کانال دارای مدلاسیون ASK می باشد. در نتیجه سیگنال حاصل معادل یک سیگنال ادغامی ASK ,PSK خواهد شد .
در همه روش های بالا ، هر کدام از مشخصه های فاز ، فرکانس و دامنه به صورت الگوی واحدی از بیت های بایندی عمل می کنند.
اگر الفبا شامل
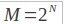
سنبل متناوب باشد ، هر سَمْبُل پیغام حاوی N بیت است . اگر نرخ سمبل را با
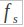
که بر حسب ( Symbole/ Second یا Boud باشد نرخ داده
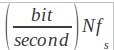
خواهد بود .
برای مثال یک الفبای شامل 16 سمبل متناوب ، هر سمبل نماینده ی 4 بیت است .
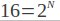 | N=4⇒ | M=16 |
در مدلاسیون های ASK ,PSK یا QAM، فرکانس حامل سیگنال مدوله شده ثابت است .
مطالب مهم عملکرد مدلاتور و دِتکتور
ASK , PSK و نیز FAK معمولاً با استفاده از QAM تولید و کشف می شوند .
اگر سیگنال کسینوسی با فاز معلوم داشته باشیم و آن را Q بنامیم و سیگنال دیگر سینوسی با 1/4 فاز قبلی داشته باشیم و آن را I بنامیم می توان این دو سیگنال را به یک سیگنال Complex _Valued ادغام کرد.
که این سیگنال I+jqQ خواهد بود ( که در آن j واحد موهومی است ) . در نتیجه سیگنال را می توان سیگنال پایین گذر هم ارز یا سیگنال باند پایه ی هم ارز نامید که معرف سیگنال مدوله شده real-valued می باشد . ( این سیگنال باند عبوری یا سیگنال RF نامیده می شود .)
یکی از مولاسیون های موسوم در ارسال در یافت رادیوی استفاده از BPSK می شود که توضیهای در این باره بیان می شود .
کلید زنی شیفت ـ باینری فازی (BPSK)
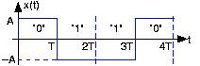
یک مثال معمول استفاده از سیگنال پالس با فرکانس ثابت که می تواند منفی یا مثبت باشد :
که در شکل زیر نشان داده شده است :
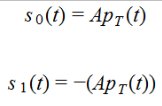
در اینجا ما یک سیگنال باند پایه مناسب برای ارسال داریم . کل گروه بیتی با
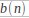
نمایش داده شده است . که نماینده ی سیگنال ای متوالی است . با توجه به قوانین ریاضی سگنال انتقال داده شده به فرم زیراست :
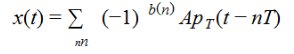
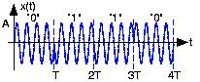
و نمودار آن در شکل زیر به نمایش در آمده است :
این راه نمایش دادن رشته ی بیت است . تغییرات بیت سبب تغییرات سیگنال ارسالی می شود که در شکل بالا نشان داده شده است ، که شکل (b) به عنوان سیگنال BPSK شناخته می شود .
میزان نرخ داده (R) یک سیستم ارتباطی دیجیتال بستگی به این دارد که بیت های اطلاعات چگونه ارسال شده باشد که در این مثال مساوی با معکوس فاصله بین هر ارسال هر بیت است (
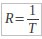
) بنا بر این برای 1Mbps ارسال داده ، ما باید T=1µSداشته باشیم .
در زیر بلوک دیا گرام یک سیستم تولید کننده مدلاسیون BPSK به طور کلی نمایش داده شده است :
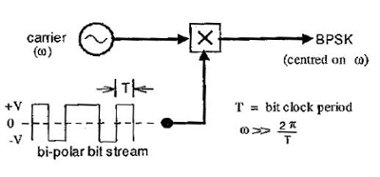
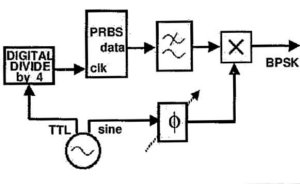
منبع: سایت پروژه های نایاب

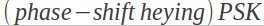
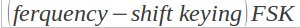
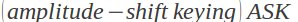
.JPG)